В туристском походе, путешествии и в других случаях часто возникает потребность в определении расстояний до недоступных предметов, измерении их длины и высоты; в определении ширины реки или другого препятствия; в определении высоты дерева; в подсчете оставшегося пути до конечной цели и т. д.
В войсковой практике, где при вычислениях постоянно приходится пользоваться соотношениями между угловыми и линейными величинами, вместо градусной системы мер применяется артиллерийская (линейная), более простая и удобная для быстрых приближепных вычислений. За единицу угловых мер артиллеристы принимают центральный угол круга, стянутого дугой, равной длины окружности. Этот угол называется делением угломера (так как используется во всех артиллерийских угломерных приборах). Иногда этот/угол называют тысячной. Это название объясняется тем, что длина дуги такого угла по окружности равна приближенно тысячной доле ее радиуса. Это очень важное обстоятельство.
Следовательно, при наблюдении окружающих нас объектов (целей, ориентиров и т. п.) мы находимся как бы в центре концентрических окружностей, радиусы которых равны расстояниям до объектов. И мерой центральных углов будут служить линейные отрезки, равные тысячной доле расстояния до объектов. Так, если дом длиной 5 м расположен на удалении от наблюдателя на 1000 м, то он укладывается в центральный угол, равный пяти тысячным. Такой угол записывается на бумаге так: 0—05 (читается: ноль, ноль пять). Если длина забора равна 100 м, то он укладывается в центральный угол, равный 100 тысячным (одно большое деление угломерного прибора). Записывается этот угол на бумаге так: 1—00 (и читается: один, ноль). Из этих примеров видно, что углы позволяют очень быстро и легко посредством простейших арифметических действий переходить из угловых измерений к линейным и обратно.
Так, например, если рядом с домом, находящимся от наблюдателя на расстоянии Д-1500 м (Д — дистанция) находится дерево и угол между ними укладывается в пятьдесят пять тысячных — У = 0—55 (У — угол) и требуется определить расстояние от дома до дерева — В (В — расстояние), то из пропорции В : Д = У : 1000 вытекает формула для определения линейных размеров.
Решим пример. У столба высотой 6 м вы видите человека. Требуется определить расстояние до него.
Вначале определяем, в какой угол укладывается высота столба. Допустим, что высота столба укладывается в угол У=0—05 (пять тысячных). Использование двух вышеприведенных формул позволяет определять быстро и точно любые линейные и угловые величины на местности.
Между делениями угломера (в тысячных) и обычной градусной системой угловых мер существуют соотношения: одна тысячная 0—01 равна 3,6′ (минуты), а большое деление угломера (1—00) =6°. Эти соотношения позволяют при необходимости осуществлять переход от одной системы измерений к другой.
Рассмотрим простейшие способы измерения углов на местности.
Их можно измерять с помощью полевого бинокля, линейки и подручных предметов.
 |
В поле зрения бинокля (рис. 13) имеются две взаимно-перпендикулярные угломерные шкалы для измерения горизонтальных и вертикальных углов. Величина одного большого деления этих шкал соответствует 0—10, а малого 0—05 тысячных. Для измерения угла между двумя направлениями надо, глядя в бинокль, совместить какой-либо штрих угломерной шкалы с одним из этих направлений и подсчитать число делений до второго направления. Так, например, на рисунке 13 отдельное дерево (пулемет противника) расположено влево от дороги на угол 0—30.
Вертикальной шкалой пользуются при определении вертикальных углов; в случае их больших размеров можно пользоваться и горизонтальной шкалой (повернув бинокль вертикально).
При отсутствии бинокля углы можно измерять обычной линейкой с миллиметровыми делениями. Если такую линейку держать перед собой на расстоянии 50 см от глаз (рис. 14), то одно деление ее (1 мм) будет соответствовать углу в две тысячных (0—02).

Точность измерения углов таким способом зависит от навыка в вынесении линейки точно на 50 см от глаза. Этого можно достигнуть, привязав к линейке ниточку и закусив ее зубами на расстоянии 50 см.
С помощью линейки можно измерять углы и в градусах. В этом случае ее следует выносить на расстояние 60 см от глаза. Тогда 1 см на линейке будет соответствовать углу в Г.
При отсутствии линейки с делениями можно использовать пальцы, ладонь или любой небольшой предмет (спичечную коробку, карандаш), размер которых в миллиметрах, а следовательно, и в тысячных известен (рис. 15). Такая мерка выносится на расстояние 50 см от глаза и по ней путем сравнения определяется искомая величина угла.
Для приближенного определения расстояний на местности используются следующие простейшие способы: глазомерный, по измеренным угловым величинам местных предметов, промером шагами, по времени движения, по звуку и вспышке от выстрела, на слух.
Глазомерный способ — основной, самый простой и быстрый, наиболее доступный каждому в любых условиях. Однако точный глазомер приобретается не сразу; он вырабатывается путем систематической тренировки, проводимой в разнообразных условиях местности, в различное время года и суток.
Чтобы развить свой глазомер, необходимо как можно чаще упражняться в определении на глаз расстояний с обязательной проверкой их шагами, по карте или другим способом.
Тренировку надо начинать с коротких расстояний (10, 50, 100 м). Хорошо освоив эти дистанции, можно переходить последовательно к большим (200, 400, 800, 1000 м). Потом можно легко определять расстояния и большие.
На точность глазомерного способа указывают такие побочные явления, как:
— более крупные предметы кажутся всегда ближе мелких, расположенных на том же расстоянии;
— чем меньше промежуточных предметов находится между глазом и наблюдаемым предметом, тем этот предмет кажется ближе;
— при наблюдении снизу вверх, от подошвы горы к вершине, предметы кажутся ближе, а при наблюдении сверху вниз — дальше.
Глазомерная оценка расстояний может контролироваться, когда несколько человек измеряют одну и ту же дистанцию независимо друг от друга. Беря среднее из всех этих определений, получают наиболее точный замер.
Для грубой оценки расстояний иногда пользуются примерными данными, приведенными в таблице 1.
| Объекты и признаки | Расстояние, с которого они становятся видимыми (различимыми) | |
| 1 | Отдельный небольшой дом, изба | 5 км |
| 2 | Труба на крыше | 3 км |
| 3 | Самолет на земле, танк на месте | 1,2 км |
| 4 | Стволы деревьев, километровые стол- | |
| бы и столбы линий связи | 1,0 км | |
| 5 | Движение ног и рук бегущего или | |
| идущего человека | 700 м | |
| С | Переплеты оконных рам | 500 м |
| 7 | Лицо человека, части его одежды | 250—300 м |
| 8 | Черепица на крышах, листья на де- | |
| ревьях | 200 м | |
| 9 | Пуговицы и пряжки, подробности | |
| вооружения | 150—170 м | |
| 10 | Черты лица человека, кисти рук | 100 м |
Каждый может уточнить и дополнить эту таблицу применительно к своим наблюдениям.
Точность глазомерного способа зависит от натренированности наблюдателя, от величины определяемых расстояний и от условий наблюдения. Для расстояний до 1000 м надо добиться тренировкой определения величин с ошибкой не более 10—15%.
Если известна линейная величина наблюдаемого предмета (высота, ширина или длина), то для определения расстояния до него необходимо измерить угол (в тысячных), под которым виден этот предмет. И по соотношению линейной (известной заранее) и угловой (измеренной) величин этого предмета, по вышеуказанной формуле можно определить расстояние до него.
При измерении расстояний шагами надо натренироваться в ходьбе ровным шагом, особенно в неблагоприятных условиях (на подъемах и спусках, при движении по кочковатому лугу, в кустарнике и т. д.). Кроме того, надо знать длину своего шага в метрах; она определяется из промера шагами линии, длина которой известна заранее и должна быть не менее 200—300 м.
При измерении расстояний шаги считают парами (обычно под левую ногу). После каждой сотни пар шагов счет начинается снова. Чтобы не сбиться со счета, полезно каждую пройденную сотню пар шагов отмечать на бумаге или же загибать последовательно пальцы рук.
Ошибки определения расстояний шагами, при ровном хорошо выверенном шаге, в среднем достигают 2—4% измеренного расстояния.
Определять расстояния можно по времени движения, если вы приблизительно знаете свою среднюю скорость движения. Так, например, если средняя скорость движения походным шагом равна 5 км/час (когда подъемы д спуски не более 5°), то, пройдя 45 минут по времени, можно ориентировочно сказать, что вами пройдено 3,75 км.
Определение расстояний до стреляющих орудий основано на обнаружении, в момент выстрела, вспышки и образования дыма. Затем, зная, что скорость распространения звука в воздухе равна 330 м/сек, то есть округленно 1 км за 3 сек, отсчитываем время в секундах от момента вспышки до момента слухового восприятия звука выстрела (или взрыва) и, поделив его на три, определяем расстояние до орудий в километрах. При отсутствии часов отсчитывать секунды можно путем порядкового счета «про себя» двухзначных чисел (21, 22, 23, 24…), начиная с момента вспышки от выстрела до прихода звука от нее. Отсчет каждого из этих чисел занимает примерно одну секунду. Навыки такого счета, соразмерного ходу секундной стрелки, довольно быстро приобретаются уже после 2— 3 тренировок в отсчете двухзначных чисел.
Ночью в условиях плохой видимости расстояния часто приходится оценивать на слух. Для этого надо уметь определять по характеру звуков их источники и знать, с каких примерно расстояний можно услышать эти звуки.
При нормальном слухе и благоприятных акустических условиях дальность слышимости можно приближенно считать такой, какой она дана в таблице 2.

Эти данные меняются в зависимости от конкретных условий, в которых производится наблюдение, поэтому должны учитываться каждым наблюдателем на основе его личного опыта.
Расскажем о некоторых прикладных измерениях на местности: дальность видимого горизонта, определение высоты дерева, определение ширины реки.
Для того чтобы лучше развить глазомер, необходимо знать, как далеко лежит от наблюдателя горизонт.
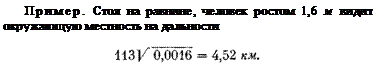
где h — высота наблюдателя (в км).
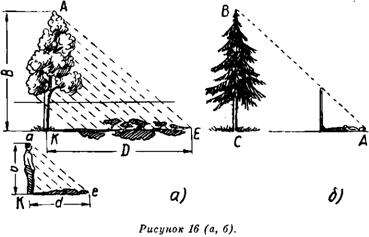
Сидя в лодке и возвышаясь над водой только на 1 м, человек может обозревать окружающую местность на дальности
![]()
Высоту дерева или любого предмета можно определить по тени, шесту, лужице или зеркальцу и треугольнику (рис. 16 а, б, в, г).
Если на ровном месте измерить шагами длину своей тени (рис. 16, а), а затем длину тени, отбрасываемой деревом (предметом), то искомую высоту легко вычислить из пропорции:
![]()
где АК — высота дерева (В); КЕ — тень дерева (D);
ак — ваш рост (6); ке — ваша тень (d).
Пример. Длина вашей тени d равна трем шагам, тень дерева Д равна 9 шагам, то есть тень дерева длиннее вашей тени в три раза. Если принять ваш рост 1,5 м, то высота дерева будет В = 1,5 X 3 = 4,5 м.

Этот же способ можно применить при пасмурной погоде, когда тени от предметов не видны. В этом случае для измерения нужно взять шест, равный длине вашего роста (рис. 16, б). Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева равна расстоянию от вашей головы до основания дерева, как это видно из рисунка, то есть АС = ВС.
По лужице и зеркальцу высоту дерева (предмета) можно измерять следующим образом. Станьте так, чтобы лужица поместилась между вами и деревом (В). Найдите точку, из которой видна отраженная в воде вершина дерева. Измеряемое дерево будет во столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше расстояния от лужицы до вас (АО). Вместо лужицы можно воспользоваться зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.
С помощью прямоугольного треугольника с двумя острыми углами по 45° высоту дерева (предмета) определяют так. Отходя от дерева на некоторое расстояние и прикладывая треугольник к глазам так, чтобы один из его катетов был параллелен оси дерева, второй — параллелен земной поверхности, а гипотенуза представляла собой
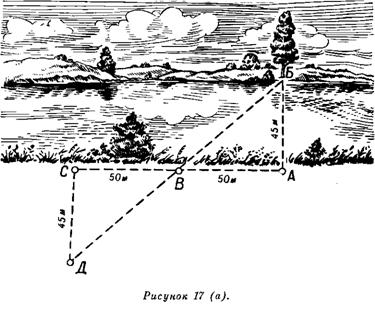
линию визирования, добиваются такого положения, чтобы линия визирования прошла через вершину дерева (рис. 16, г). В этом случае высота дерева Д равна расстоянию от наблюдателя до дерева и плюс рост наблюдателя.
Ширину реки определяют следующим образом. Наблюдатель становится на берегу реки в точке А (рис. 17, а) и выбирает на противоположном берегу какой-либо хорошо заметный ориентир (куст, камень, дерево и т. п.). После этого, идя в направлении, перпендикулярном к линии АБ, переходит в точку В, удаленную от точки А больше, чем предполагаемая ширина реки. В точке В устанавливает веху (палку, колышек и т. п.), затем, идя по тому же направлению, переходит в точку С, которая находится от точки В на таком же расстоянии, как и точка В от точки А. Далее от точки С идет под прямым углом к линии АС до точки Д, то есть до тех пор, пока веха, установленная в точке В, не окажется в створе с выбранным ориентиром (деревом) на противоположном берегу. Из равенства тре-
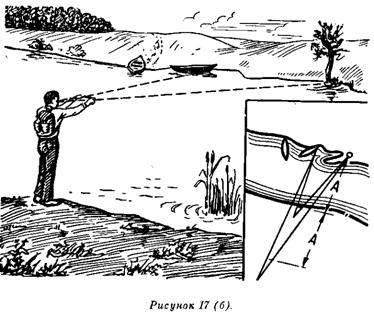
угольников ВДС = ВБА видно, что отрезок СД = АБ, то есть ширине реки. В нашем примере на рисунке он равен 45 м.
Ширина реки может быть определена и с помощью травинки. Сорвите ее и выберите на противоположном берегу реки два заметных предмета. Встаньте лицом к этим предметам, вытяните руки с травинкой и отмерьте с помощью ее расстояние между предметами, смотря на них одним глазом (любым). После этого сложите травинку пополам (вдвое) и отходите от берега до тех пор, пока расстояние между выбранными предметами не закроется (не уложится) сложенной вдвое травинкой. Замерьте это расстояние шагами, переведите его в метры — это и будет расстояние, равное ширине реки (рис. 17, б).
Определить крутизну скатов в полевых условиях очень важно при оценке проходимости местности.
Для того чтобы оценивать крутизну скатов на глаз, надо изучить на местности и закрепить в зрительной памяти крутизну нескольких типичных скатов (15°, 30°, 45°,

60°), а затем путем мысленного сравнения с ними определять крутизну других скатов.
Следует всегда помнить, что снизу, от подошвы возвышенности, скат всегда кажется круче, чем в действительности.
Более точные результаты получаются, если, зайдя сбоку ската, сравнить его на глаз с величиной какого-либо имеющегося целлулоидного треугольника, величины углов которого известны.
Измерив заранее углы между расставленными возможно шире большим, указательным и средним пальцами руки, можно пользоваться и этими углами для оценки на глаз крутизны скатов.
Крутизну ската можно определять и промером шагов по приближенной формуле:
![]()
где ПШ — протяженность ската, измеренная парами шагов.
Для определения по этой формуле крутизны скатов наблюдатель становится в точке А (рис. 18, а) и, держа на уровне глаз горизонтально папку или книжку, смотрит вдоль нее и замечает на скате точку С, равную по высоте наблюдателя до уровня глаз. Затем, двигаясь по направле-
нию к этой точке, измеряют число пар шагов и по формуле определяют крутизну ската.
Пример. От точки А до точки С отсчитано 4 пары шагов.
![]()
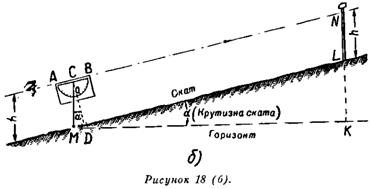
Крутизну скатов можно замерять с помощью эклиметра — угломерного прибора для измерения наклона линий местности к горизонту (рис. 18, б).
Чтобы определить крутизну ската с помощью эклиметра, его держат на уровне глаз так, чтобы линия основания АВ была параллельна направлению ската (обычно ставят на определенном расстоянии веху с отметкой высоты расположения глаз наблюдателя). Тогда нить отвеса эклиметра покажет угол, равный углу крутизны ската. Самодельный эклиметр можно выполнить с помощью простого транспортира. К полочке транспортира в центре (посредине) привязывают ниточку с грузиком и, переворачивая транспортир вверх полочкой, направляют ее ребро параллельно боковой поверхности ската. Ниточка с грузом отклоняется от деления 90° на шкале транспортира на угол, равный крутизне ската.
Таковы те простейшие способы измерений на местности, которыми должен владеть каждый школьник.









